Building upon our recent series of blog posts on fiber-coupled diode lasers, we now turn our attention to how you can manipulate the laser light coming out of a fiber. Perhaps the most common question we get here at RPMC, is how to get a specific laser spot size at a given distance. This seemingly simple question of “which lens should I use?” or “how to get the right laser spot at the right distance?” is actually a rather complex problem that is highly dependent on the particular type of fiber-optic. For example, when working with a single-mode fiber, it is essential to recognize that the output is exceptionally close to that of a Gaussian beam (M2 » 1.05), and therefore traditional geometric optical equations will break down. Additionally, on the other extreme when dealing with large-core multimode fibers where the output can be viewed as a relatively flat-top beam profile to enable the use of basic geometric optics. The large size of the core means that the laws of conservation of brightness (also known as etendue) dramatically reduces the minimum achievable spot size.
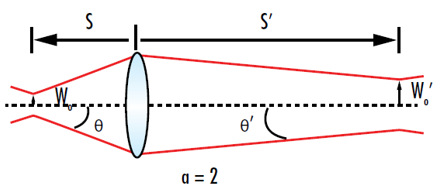
Let’s start by taking a look at the output of a single-mode fiber-coupled diode laser. While a detailed explanation of Gaussian optics is beyond the scope of this article, the diagram below does an excellent job of showing the relationship between the initial spot radius (wo) and the final spot radius (wo’) after imaging for a Gaussian beam. When applied to our specific case of imaging, the output of a fiber-coupled lasers diode, wo is equal to the core radius, and wo’ would be the radius of the spot size at a distance s’ from the lens.
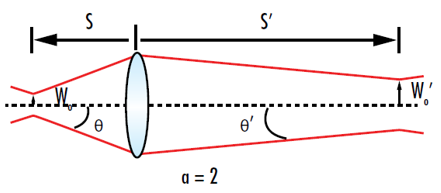
For a detailed derivation of how to find wo’, we recommend checking out Edmund Optics’ application note on Gaussian beam optics by clicking here. But for the sake of this blog post we will jump right to the result that wo’ = (f × wo)/|s|, which when combined with the imaging equation for a Gaussian beam, s’= f2+f2/|s| allows you to figure out the spot size you will get at a given distance for a given focal length lens. For example, if a 785 nm single-mode fiber-coupled laser with a core diameter of 5 microns is imaged with a 10mm lens placed at a distance of 5mm in front of the fiber, it will result in a 10-micron diameter spot at a distance s’ of 30mm in front of the lens. As a general rule, you should always keep in mind that when imaging a laser, the shorter the focal length of the lens the smaller the resultant laser spot.
Another relevant example is to look at what happens when s = f, which means that the lens is placed one focal length in front of the fiber. In this case, s’ goes to infinity which means that the output would be collimated. In this case if the numerical aperture of the lens and the fiber are the same then the output beam will be equal to the diameter of the lens at all locations. But, as a general rule of thumb, you typically want to pick a lens with a slightly larger numerical aperture to avoid any vignetting and aberrations from the edges of the collimating lens. For example, if you are using a single-mode fiber with a numerical aperture of .13, you would most likely pick a collimating lens with a numerical aperture of 0.15. It is important to note though, that this approximation ignores any aberrations introduced by the lens. Luckily when dealing with infinite conjects (collimated light) aspheric lenses do not add any spherical aberration. Additionally, since the output will be collimated (e.g. all of the rays are parallel to the optical axis) as long as the lens is aligned correctly, there will also be no off-axis aberrations such as coma or astigmatism. Therefore, whenever you are collimating a single-mode laser beam with an aspheric lens the result will be diffraction-limited collimation.
For the sake of brevity, we will leave the discussion of the beam properties of multimode fiber-coupled diode lasers for the second part of this series coming out next month. In the meantime, if you would like to get more detailed information on the fiber-coupled diode lasers offered here at RPMC Lasers, click here or, you can also talk to one of our laser experts today by calling 1-636-272-7227.

 SHIPS TODAY
SHIPS TODAY 